极惯性矩
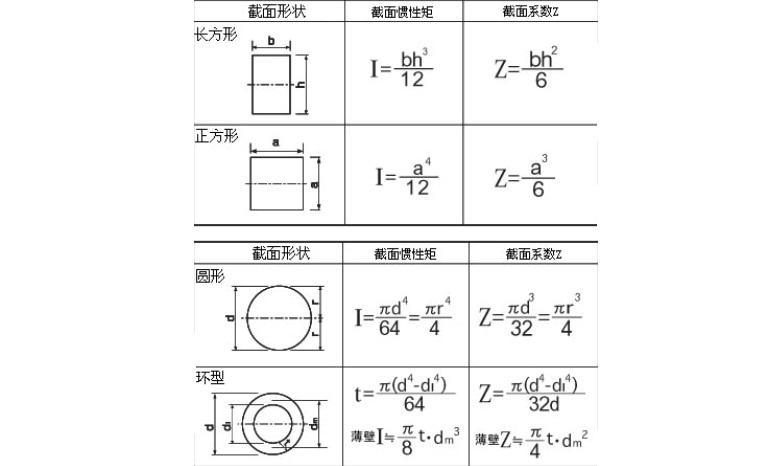
编辑面积的第二极矩,也称为(错误地,口语化地)极惯性矩或惯性矩,是用于描述圆柱形(或非圆柱形)物体(或 物体的部分)具有不变的横截面并且没有明显的翘曲或平面外变形。 它是面积二阶矩的组成部分,通过垂直轴定理联系起来。 其中平面面积二阶矩描述物体在受到施加到平行于中心轴的平面上的力时对偏转(弯曲)的抵抗力,面积的极坐标二阶矩描述物体在以下情况下对偏转的抵抗力 受到在垂直于物体中心轴(即平行于横截面)的平面上施加的力矩。
简而言之,“区域极矩”是轴或梁抗扭转变形的能力,是其形状的函数。 刚度仅来自物体的横截面积,而不取决于其材料成分或。 面积二次极矩的大小越大,物体的扭转刚度就越大。
定义
编辑描述面积极矩的方程是物体横截面积 A {dISPlaystyle A} 的多重积分。
这也显示在垂直轴定理中。 对于具有旋转对称性的物体,例如圆柱体或空心管
单位
编辑与面积的平面二次矩一样,极地二次矩的 SI 单位在美国惯用单位和英制单位中是米的四次方 (m4) 和英寸的四次方 (in4)。
限制
编辑面积的极二次矩不足以用于分析具有非圆形横截面的梁和轴,因为它们在扭曲时倾向于翘曲,从而导致面外变形。 在这种情况下,应该用扭转常数代替,其中包括适当的变形常数以补偿翘曲效应。 其中,有文章区分了面积的极二矩 I z {diSPlaystyle I_{z}} 和扭转常数 J t {displaystyle J_{t}} ,不再使用 J { displaystyle J} 来描述面积的极二矩。
在具有显着横截面变化(沿施加扭矩的轴)的物体中,无法分段分析,可能必须使用更复杂的方法。 请参见 3-D 弹性。
申请
编辑虽然极坐标二次矩最常用于计算物体在平行于横截面施加的力矩(扭矩)下的角位移,但提供的刚度值与提供的抗扭阻力没有任何关系 一个物体作为其组成材料的函数。 物体材料提供的刚度是其剪切模量 G {displaystyle G} 的一个特征。 将这两个特征与轴的长度 L {displaystyle L} 结合起来,就能够计算出轴的角度偏转 θ {displaystyle theta } 。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214297/
