简介
编辑与弹性碰撞相反,非弹性碰撞是由于内摩擦的作用而导致动能不守恒的碰撞。
宏观物体碰撞时,部分动能转化为原子的振动能,产生热效应,物体发生变形。
气体或液体的分子很少经历完美的弹性碰撞,因为动能在分子的平移运动和它们的内部自由度之间交换,每次碰撞。 在任何一个瞬间,一半的碰撞——在不同程度上——是非弹性的(碰撞后的动能比碰撞前的小),一半可以被描述为“超弹性”(碰撞后的动能比碰撞前的多) 前)。 平均整个样本,分子碰撞是弹性的。
尽管非弹性碰撞不守恒动能,但它们确实服从动量守恒。 简单的弹道摆问题仅在木块摆动到最大角度时服从动能守恒。
在核物理学中,非弹性碰撞是指入射粒子导致其撞击的原子核被激发或破裂的碰撞。 深度非弹性散射是一种探测亚原子粒子结构的方法,其方式与卢瑟福探测原子内部的方式非常相似(请参阅卢瑟福散射)。 此类实验是在 1960 年代后期在斯坦福直线加速器 (SLAC) 上使用高能电子对质子进行的。 与卢瑟福散射一样,质子靶对电子的深度非弹性散射表明,大多数入射电子相互作用很小,直接通过,只有一小部分反弹回来。 这表明质子中的电荷集中在小块中,让人想起卢瑟福发现原子中的正电荷集中在原子核上。 然而,就质子而言,证据表明存在三种不同的电荷浓度(夸克),而不是一种。
公式
编辑一维碰撞后的速度公式为: {aligned}v_{a}&={frac {C_{R}m_{b}(u_{b}-u_{a})+m_{a}u_{a}+m_{b}u_{ b}}{m_{a}+m_{b}}}v_{b}&={frac {C_{R}m_{a}(u_{a}-u_{b}) +m_{a}u_{a}+m_{b}u_{b}}{m_{a}+m_{b}}}end{对齐}}}
在哪里
- va 是第一个物体撞击后的最终速度
- vb 是第二个物体撞击后的最终速度
- ua 是第一个物体撞击前的初始速度
- ub 是第二个物体撞击前的初速度
- ma 是第一个物体的质量
- mb 是第二个物体的质量
- CR 是恢复系数; 如果它是 1,我们有一个弹性碰撞; 如果它是 0,我们有一个完全非弹性碰撞,见下文。
在动量中心框架中,公式简化为:
v a = − C R u a v b = − C R u b {dISPlaystyle {begin{aligned}v_{a}&=-C_{R}u_{a}v_{b}&=-C_{ R}u_{b}end{对齐}}}
对于二维和三维碰撞,这些公式中的速度是垂直于接触点切线/平面的分量。
如果假设物体在碰撞之前或之后没有旋转,则正常冲量为:
J n = m a m b m a + m b ( 1 + C R ) ( u b → − u a → ) ⋅ n → {diSPlaystyle J_{n}={frac {m_{a}m_{b}}{m_{a}+ m_{b}}}(1+C_{R})({vec {u_{b}}}-{vec {u_{a}}})cdot {vec {n}} }
其中 n → {displaystyle {vec {n}}} 是法向量。
假设没有摩擦,这给出了速度更新:
Δ v a → = J n m a n → Δ v b → = − J n m b n → {displaystyle {begin{aligned}Delta {vec {v_{a}}}&={frac {J_{ n}}{m_{a}}}{vec {n}}Delta {vec {v_{b}}}&=-{frac {J_{n}} {m_{b}}}{vec {n}}end{对齐}}}
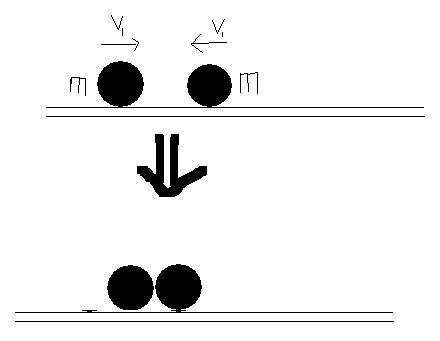
完全非弹性碰撞
编辑当系统失去最大动能时,就会发生完全非弹性碰撞。在完全非弹性碰撞中,即零恢复系数,碰撞粒子粘在一起。在这样的碰撞中,动能通过将两个物体结合在一起而损失。这种结合能通常导致系统的最大动能损失。有必要考虑动量守恒:(注意:在上面的滑块示例中,只有当表面摩擦力为零时,两个物体系统的动量才守恒。有摩擦力,两个物体的动量转移到表面 两个物体在上面滑动。同样,如果存在空气阻力,则物体的动量可以传递到空气中)。下面的等式适用于上例中的双体(Body A,Body B)系统碰撞 。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214341/
