瑞利-贝纳德对流
编辑在流体热力学中,瑞利-贝纳德对流是一种自然对流,发生在从下方加热的平面水平流体层中,其中流体形成规则的对流单元模式,称为贝纳德单元。 Bénard-Rayleigh 对流是最常研究的对流现象之一,因为它具有分析和实验可及性。 对流模式是自组织非线性系统经过最仔细检查的示例。
浮力和重力是造成对流细胞出现的原因。 最初的运动是密度较低的流体从较暖的底层上升流。 这种上升流自发地组织成规则的细胞模式。
物理过程
编辑贝纳德对流的特征可以通过法国物理学家亨利·贝纳德于 1900 年首先进行的一个简单实验得到。
对流的发展
编辑实验装置使用一层液体,例如 水,在两个平行平面之间。 与水平尺寸相比,层的高度很小。 起初,底部平面的温度与顶部平面相同。 然后液体将趋于平衡,其温度与周围环境相同。 (一旦到达那里,液体是完全均匀的:对于观察者来说,从任何位置看起来都是一样的。这种平衡也是渐近稳定的:在外部温度的局部暂时扰动之后,它会回到均匀状态,在 符合热力学第二定律)。
然后,底部平面的温度略有增加,产生通过液体传导的热能流。 该系统将开始具有导热结构:温度、密度和压力将在底部和顶部平面之间线性变化。 将建立均匀的线性温度梯度。 (该系统可以通过统计力学建模)。
一旦建立传导,微观随机运动自发地在宏观层面上变得有序,形成贝纳德对流单元,具有特征相关长度。
对流特征
编辑细胞的旋转是稳定的,水平方向会顺时针到逆时针交替; 这是自发对称性破缺的一个例子。 Bénard 细胞是亚稳态的。 这意味着小的扰动将无法改变细胞的旋转,但较大的扰动可能会影响旋转; 它们表现出一种滞后现象。
此外,微观层面的确定性规律产生了细胞的非确定性排列:如果重复实验,实验中的特定位置在某些情况下会在顺时针细胞中,而在其他情况下会在逆时针细胞中。 初始条件的微观扰动足以产生不确定的宏观效应。 也就是说,原则上无法计算微观扰动的宏观效应。 这种无法预测长期条件和对初始条件的敏感性是混沌或复杂系统的特征(即蝴蝶效应)。
如果进一步提高底面的温度,结构在空间和时间上将变得更加复杂; 湍流将变得混乱。
对流 Bénard 细胞倾向于近似规则的直角六角棱柱,特别是在没有湍流的情况下,尽管某些实验条件可能导致形成规则的直角棱柱或螺旋。
对流 Bénard 细胞不是唯一的,通常只出现在表面张力驱动的对流中。 一般来说,假设无限水平层的瑞利和皮尔逊分析(线性理论)的解决方案会导致退化,这意味着系统可能会获得许多模式。 假设顶板和底板的温度均匀,当使用现实系统(具有水平边界的层)时,边界的形状将决定图案。 通常情况下,对流会表现为滚动或它们的叠加。
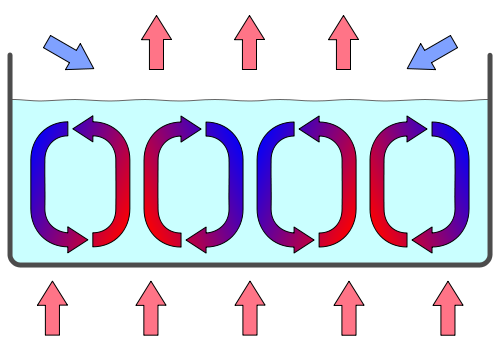
瑞利-贝纳德不稳定性
编辑由于顶板和底板之间存在密度梯度,重力会试图将温度较低、密度较大的液体从顶部拉到底部。 该重力与流体中的粘性阻尼力相反。 这两个力的平衡由称为瑞利数的无量纲参数表示。
Tu 是顶板的温度 Tb 是底板的温度 L 是容器的高度 g 是重力加速度 ν 是运动粘度 α 是热扩散系数 β 是热膨胀系数。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216498/
