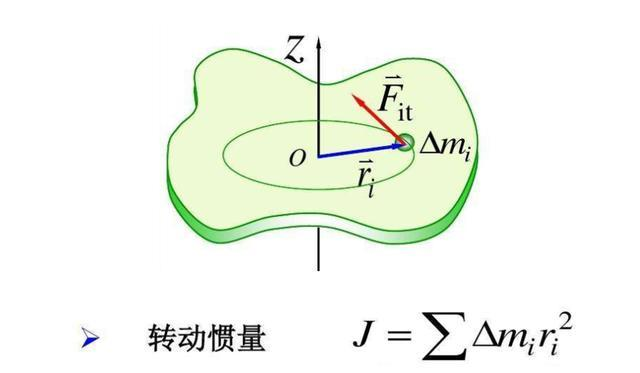
转动惯量

惯性矩，也称为刚体的质量惯性矩、角质量、第二质量矩，或更准确地说，转动惯量，是确定绕旋转轴的所需角加速度所需扭矩的量 ，类似于质量如何决定所需加速度所需的力。 转动惯量是一个标准的机械量。 这取决于身体的质量分布和所选的轴，力矩越大，需要越大的扭矩来改变身体的旋转速度。

这是一个广泛的（附加的）属性：对于点质量，惯性矩只是质量乘以到旋转轴的垂直距离的平方。 刚性复合系统的惯性矩是其组件子系统的惯性矩之和（全部围绕同一轴）。 其最简单的定义是相对于与轴的距离的质量二次矩。

对于被迫在平面内旋转的物体，只有它们绕垂直于平面的轴的惯性矩（标量值）才重要。 对于在三个维度上自由旋转的物体，它们的力矩可以用对称的 3 × 3 矩阵来描述，该矩阵具有一组相互垂直的主轴，对于该矩阵，该矩阵是对角线的，并且绕轴的扭矩彼此独立。

当物体绕轴自由旋转时，必须施加扭矩以改变其角动量。 引起任何给定角加速度（角速度的变化率）所需的扭矩量与身体的惯性矩成正比。 惯性矩可以用 SI 单位的千克米平方 (kg·m2) 和英制或美制单位的磅-英尺·秒平方 (lbf·ft·s2) 表示。

惯性矩在旋转动力学中的作用与质量（惯性）在线性动力学中的作用相同——两者都表征了物体对其运动变化的抵抗力。 惯性矩取决于质量围绕旋转轴的分布方式，并且会根据所选轴而变化。 对于点状质量，关于某个轴的惯性矩由 m r 2 {displaystyle mr{2}} 给出，其中 r {displaystyle r} 是点到轴的距离，m { displaystyle m} 是质量。 对于一个扩展的刚体，惯性矩就是所有小质量块乘以它们到旋转轴的距离的平方的总和。 对于规则形状和均匀密度的扩展物体，这种求和有时会产生一个简单的表达式，该表达式取决于物体的尺寸、形状和总质量。

1673 年，克里斯蒂安·惠更斯 (Christiaan Huygens) 在研究悬挂在枢轴上的物体（称为复摆）的振荡时引入了该参数。 惯性矩一词由莱昂哈德·欧拉于 1765 年在他的著作 Theoria motus corporum solidorum seu rigidorum 中引入，并被纳入欧拉第二定律。

复摆的固有振动频率是通过重力施加在摆质量上的扭矩与由惯性矩定义的加速度阻力之比获得的。 将此固有频率与由单质点组成的单摆的固有频率进行比较，可以得出扩展物体惯性矩的数学公式。

惯性矩也出现在动量、动能和牛顿运动定律中，作为结合其形状和质量的物理参数。 惯性矩在平面和空间运动中的表现方式有一个有趣的区别。 平面运动有一个定义惯性矩的标量，而对于空间运动，相同的计算会产生一个 3×3 的惯性矩矩阵，称为惯性矩阵或惯性张量。

旋转飞轮的惯性矩在机器中用于抵抗施加扭矩的变化，以平滑其旋转输出。 飞机关于其纵轴、水平轴和垂直轴的惯性矩决定了机翼、升降舵和方向舵控制面上的转向力如何影响飞机的横滚、俯仰和偏航运动。

惯性矩定义为截面质量与参考轴与截面质心之间距离的平方的乘积。

转动惯量 I 也定义为系统的净角动量 L 与其绕主轴的角速度 ω 之比，即 I = L ω 。 {displaystyle I={frac {L}{omega }}。}

如果一个系统的角动量是恒定的，那么随着惯性矩变小，角速度必然增加。 当旋转的花样滑冰运动员拉回他们伸出的手臂或潜水员在潜水期间将他们的身体卷曲成折叠位置时，就会发生这种情况。