运动链简介
编辑在机械工程中,运动链是由关节连接的刚体组件,以提供受约束(或期望的)运动,这是机械系统的数学模型。 就像我们熟悉的单词链一样,刚体或链接受它们与其他链接的连接的约束。 一个例子是由串联连接的链节形成的简单开链,就像通常的链条一样,它是典型机器人机械手的运动学模型。
两个连杆之间的连接或关节的数学模型称为运动学对。 运动副对机器人技术的基础铰链和滑动关节进行建模,通常称为低副,以及对凸轮和齿轮装置至关重要的表面接触关节,称为高副。 这些关节通常被建模为完整约束。 运动图是显示运动链的机械系统示意图。
运动链的现代用途包括由精密机构中的挠性接头产生的合规性、合规机构和微机电系统中的连杆合规性,以及电缆机器人和张拉整体系统中的电缆合规性。
迁移率公式
编辑运动链的自由度或移动性是定义链配置的参数数量。在空间中移动的 n 个刚体系统相对于固定框架测量有 6n 个自由度。 该框架包含在物体的计数中,因此移动性不依赖于形成固定框架的链接。 这意味着该系统的自由度为 M = 6(N − 1),其中 N = n + 1 是移动体加上固定体的数量。
连接身体的关节会施加约束。 具体来说,铰链和滑块各施加五个约束,因此移除五个自由度。 根据关节的自由度 f 定义关节施加的约束数 c 很方便,其中 c = 6 − f。 对于单自由度铰链或滑块,f = 1,因此 c = 6 − 1 = 5。
回想一下,N 包括固定链路。
运动链分析
编辑运动链的约束方程将每个关节允许的运动范围与链中链节的尺寸相结合,并形成代数方程,求解这些方程以确定与输入参数的特定值相关联的链的配置,称为度数 的自由。
运动链的约束方程是使用刚性变换 [Z] 获得的,以表征每个关节处允许的相对运动,并使用单独的刚性变换 [X] 来定义每个链接的尺寸。 在串行开放链的情况下,结果是一系列刚性变换,从链的底部到其末端链接交替进行关节和链接变换,这等同于末端链接的指定位置。
其中 [T] 是定位末端链接的变换——请注意,该链包括第零个链接,该链接由它所连接的地面框架组成。 这些方程称为串联链的正向运动学方程。
通过使在运动链中形成回路的串行链的运动学方程相等,分析了各种复杂性的运动链。 这些方程通常称为循环方程。
链条的复杂性(在计算正向和反向运动学方面)由以下因素决定:
解释
空间中两个或多个刚体统称为刚体系统。 我们可以用运动学约束来阻止这些独立刚体的运动。 运动学约束是刚体之间的约束,导致刚体系统的自由度降低。
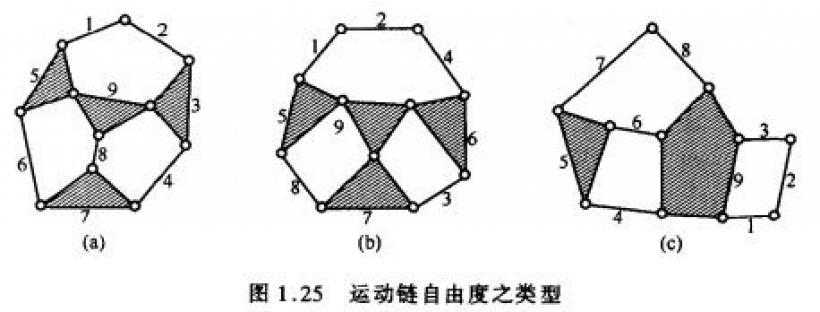
运动链的合成
编辑可以反向使用运动链的约束方程,根据系统所需运动的规范来确定链接的尺寸。 这称为运动合成。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/197991/
