简介
编辑在连续介质力学中,涡度是一个伪矢量场,它描述了某个点附近连续介质的局部旋转运动(某物旋转的趋势),正如位于该点并随流行进的观察者所看到的那样。 它是流体动力学理论中的一个重要量,为理解各种复杂的流动现象(例如涡环的形成和运动)提供了一个方便的框架。
在数学上,涡量 ω → {dISPlaystyle {vec {omega }}} 是流速 u → {diSPlaystyle {vec {u}}} 的旋度:
ω → ≡ ∇ × u → , {displaystyle {vec {omega }}equiv nabla times {vec {u}},,}
其中 ∇ {displaystyle nabla } 是 nabla 运算符。 从概念上讲,ω → {displaystyle {vec {omega }}} 可以通过在问题点的一个小邻域中标记连续体的部分,并观察它们沿流移动时的相对位移来确定。 涡量 ω → {displaystyle {vec {omega }}} 将是这些粒子相对于其质心的平均角速度矢量的两倍,根据右手法则定向。
在二维流动中,ω → {displaystyle {vec {omega }}} 总是垂直于流动平面,因此可以被认为是标量场。
例子
编辑在像刚体一样旋转的连续体质量中,涡度是旋转角速度矢量的两倍。 例如,朗肯涡旋的中心就是这种情况。
如果存在剪切(即,如果流速跨流线变化),即使所有粒子都沿着直线和平行路径流动,涡度也可能不为零。 例如,在具有恒定横截面的管道内的层流中,所有粒子都平行于管道的轴线移动; 但在该轴附近速度更快,并且几乎在墙壁旁边静止不动。 涡量在轴上为零,在切变最大的壁附近最大。
相反,流动可能具有零涡度,即使它的粒子沿着弯曲的轨迹行进。 一个例子是理想的无旋涡流,其中大多数粒子围绕某个直轴旋转,速度与它们到该轴的距离成反比。 一小块不跨轴的连续体将在一个方向上旋转,但在相反的方向上被剪切,这样它们围绕质心的平均角速度为零。
另一种可视化涡流的方法是想象,瞬间,连续体的一小部分变成固体,其余的流动消失。 如果那个微小的新固体粒子在旋转,而不是随流移动,那么流中就有涡流。
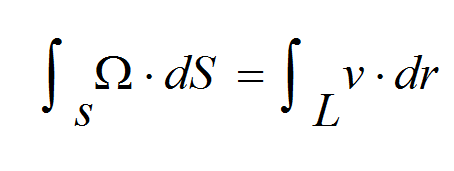
数学定义
编辑在数学上,三维流的涡度是一个伪矢量场,通常表示为 ω → {displaystyle {vec {omega }}} ,定义为速度场的旋度 v → {displaystyle {vec {v}}} 描述连续运动。
换句话说,涡度表示当一个人在垂直于它的方向上移动无穷小的距离时,速度矢量如何变化。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/214307/
