进动

进动是旋转体的旋转轴方向的变化。 在适当的参考系中，它可以定义为xxx个欧拉角的变化，而第三个欧拉角定义旋转本身。 换句话说，如果物体的旋转轴本身围绕第二个轴旋转，则称该物体绕第二个轴进动。 第二欧拉角发生变化的运动称为章动。 在物理学中，有两种类型的进动：无扭矩和扭矩引起的。

在天文学中，岁差是指天体的旋转或轨道参数的若干缓慢变化中的任何一个。 一个重要的例子是地球自转轴方向的稳定变化，称为分点岁差。

无扭矩进动意味着没有外部力矩（扭矩）施加到身体上。 在无扭矩进动中，角动量是常数，但角速度矢量随时间改变方向。 使这成为可能的是随时间变化的惯性矩，或者更准确地说，是随时间变化的惯性矩阵。 惯性矩阵由相对于单独的坐标轴计算的物体的惯性矩组成。 如果物体关于其旋转主轴不对称，则相对于每个坐标方向的惯性矩将随时间变化，同时保持角动量。 结果是身体绕每个轴的角速度分量将与每个轴的惯性矩成反比。

具有对称轴的物体围绕不与该对称轴对齐的轴旋转的无扭矩进动率可以计算如下：ωp = IsωsIpcos⁡（α ) 。 其中 ωp 是进动率，ωs 是关于对称轴的自旋率，Is 是关于对称轴的惯性矩，Ip 是关于其他两个相等垂直主轴之一的惯性矩，和 α是转动惯量方向与对称轴的夹角。

当物体不是完全固体时，内部涡流会抑制无扭矩进动，旋转轴将与物体的惯性轴之一对齐。

对于没有任何对称轴的一般固体对象，对象方向的演变由将内部坐标转换为外部坐标的旋转矩阵 R 表示，可以进行数值模拟。 给定物体的固定内部转动惯量张量 I0 和固定外部角动量 L，瞬时角速度为 ω ( R ) = R I 0 − 1 R T L，运动通过重复重新计算 ω 并在短时间 dt 内应用小旋转矢量 ω dt 而发生； 有限时间步长引起的误差往往会增加旋转动能： E ( R ) = ω ( R ) ⋅ L 2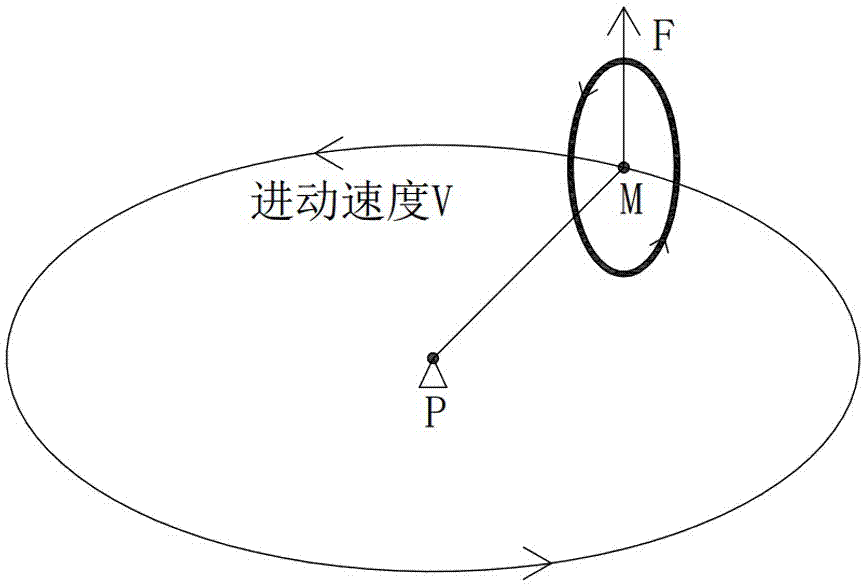

扭矩引起的进动（陀螺仪进动）是旋转物体（例如陀螺仪）的轴在施加外部扭矩时在空间中描绘一个圆锥体的现象。 这种现象在旋转的玩具陀螺中很常见，但所有旋转的物体都可以进行进动。 如果旋转速度和外部扭矩的大小是恒定的，则自旋轴将与外部扭矩直观产生的方向成直角移动。 在玩具陀螺的情况下，其重量从其质心向下作用，并且地面的法向力（反作用力）在与支撑的接触点向上推动它。